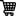A kite in the shape of a square with a diagonal 32 cm attached to an equilateral triangle of the base cm. Approximately how much paper has been used to make it?
A kite in the shape of a square with a diagonal 32 cm attached to an equilateral triangle of the base 8 cm. Approximately how much paper has been used to make it?
[A]$latex 539.217 cm^{2}$
[B]$latex 538.721 cm^{2}$
[C]$latex 540.712 cm^{2}$
[D]$latex 539.712 cm^{2}$
$latex 539.712 cm^{2}$
Area of paper = Area of square + Area of equilateral triangle
$latex = \frac{1}{2}(diagonal)^{2} + \frac{\sqrt{3}}{4}\times (side)^{2}&s=1$
$latex = \frac{1}{2}\times 32 \times 32 + \frac{\sqrt{3}}{4}\times8 \times 8&s=1$
$latex = 512 + 16 \times 1.732$
$latex = 512 +27.712 = 539.712 cm^{2}$ [∴ Diagonal of a square = $latex \sqrt{2} \times side$]
Hence option [D] is the right answer.